
Alex H. Parker
This series of 4000 figures is associated with work I published in 2008.
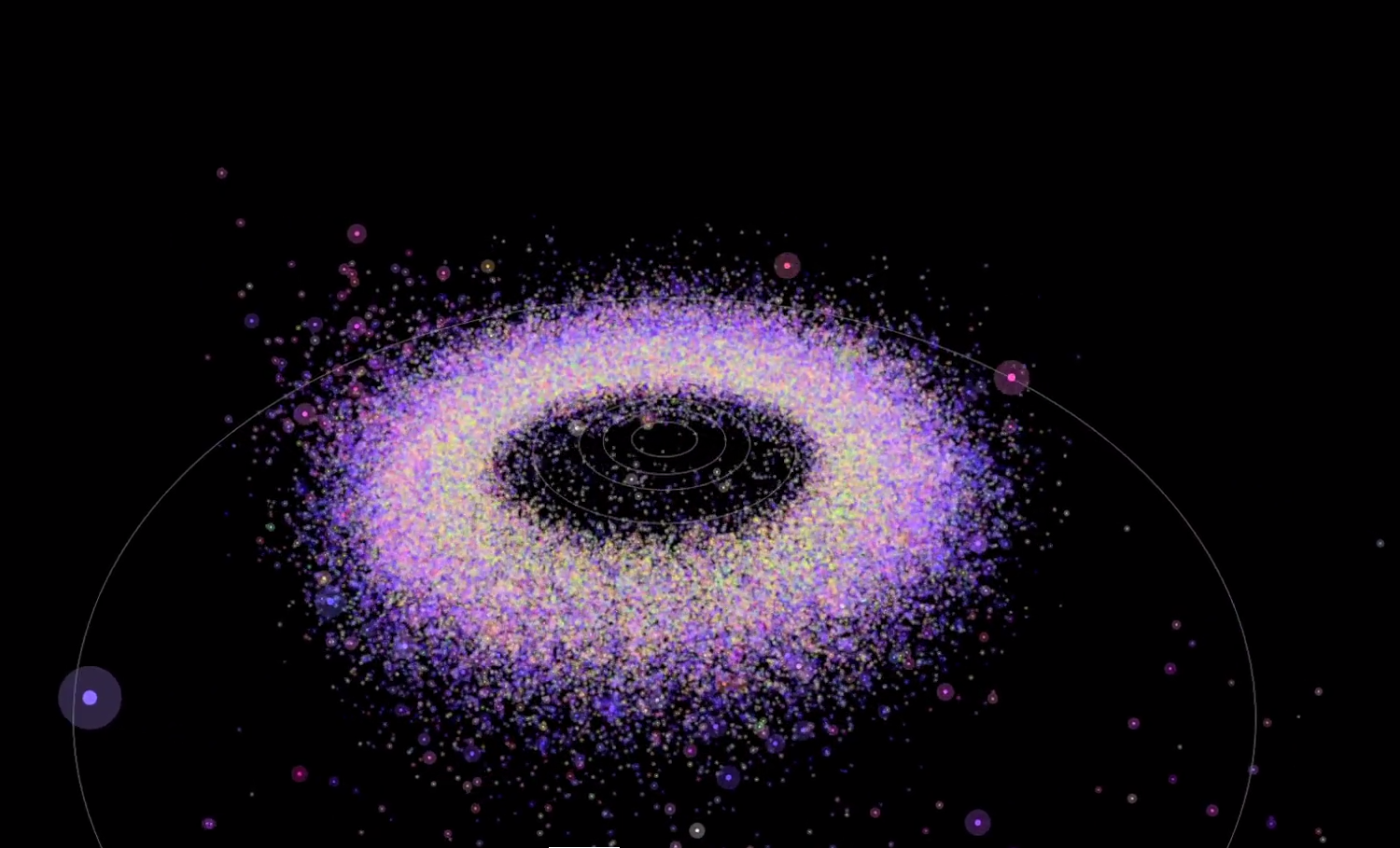
This animation shows the orbital motions of over 100,000 of the asteroids observed by the Sloan Digital Sky Survey (SDSS), with colors illustrating the compositional diversity measured by the SDSS five-color camera. The relative sizes of each asteroid are also illustrated. All main-belt asteroids and Trojan asteroids with orbits known to high precision are shown. The animation is rendered with a timestep of 3 days. The most surprising result of this animation is that compositional gradient of the asteroid belt is clearly visible, with green Vesta-family members in the inner belt fading through the pink and yellow S-class asteroids to the blue C-class asteroids in the outer belt, and onward to the deep red Trojan swarms beyond that. This gradient is easily detected when plotting the belt in its component orbital elements, but the fact that it appears in physical space as well is neatly illustrated here. Occasional diagonal slashes that appear in the animation are the SDSS survey beams; these appear because the animation is rendered at near the survey epoch.
The work is rendered in matplotlib, and demonstrates how matplotlb can produce semi-cinematic data visualizations (all the visualizations here are generated with matplotlib).
Running: Download ADR4.dat and place in working directory. On first run, ADR4_movie.py (below) will build a (huge) database containing ‘moc_orbit’ objects.
For demo purposes, simply run it as: python ADR4_movie.py 0
This will render all the frames in sequence.
#!/usr/bin/env python
""" Animates all the asteroids with reasonable orbits in the SDSS MOC4 catalog, with their mapped colors. """
__author__ = "Dr. Alex H Parker"
__email__ = "alexharrisonparker@gmail.com"
import numpy
import pylab
import math
import sys
import shelve
import os
from numpy import sin, cos, arctan, sqrt, tan, pi, arctan2
import time
from scipy.special import jv
def get_color2(a,iz):
### Generate RGB color from a* and i-z colors
### similar to Parker et al. 2008
### R determined by a*
### B determined by a*
### G determined by iz
### The following 9 parameters are adjustable.
### the cR and cB parameters adjust the location of the transition from Red to Blue
### the cG parameter adjusts the transition from (Red or Blue) to Green
cR = -0.15
cB = -0.16
cG = -0.15
### the "s" parameters adjust the relative "strength" of each group.
sR = 2.
sB = 10.
sG = 4.
### the "w" parameters adjust the width of the transition from each color group to the others
### (larger "w" means faster transition)
wR = 3.
wB = 4.
wG = 3.
###
### GENERATE THE HUES with hyperbolic tangent functions and c, s, and w parameters
###
R = sR*(math.tanh( wR*(a - cR )) + 1 )
B = sB*(math.tanh(-wB*(a - cB )) + 1 )
G = sG*(math.tanh(-wG*(iz - cG )) + 1 )
###
### NORMALIZE MAGNITUDE of (R,G,B) to 1
### (requires "math.sqrt" function be available)
###
#mag = math.sqrt( R**2 + B**2 + G**2)
mag = max( [R, G, B] )
R,G,B = R/mag, G/mag, B/mag
### return corrected (R,G,B) tuple
return R, G, B
class Point3D:
### Shamelessly borrowed from http://codentronix.com/2011/04/20/simulation-of-3d-point-rotation-with-python-and-pygame/
def __init__(self, x = 0, y = 0, z = 0):
self.x, self.y, self.z = float(x), float(y), float(z)
def rotateX(self, angle):
""" Rotates the point around the X axis by the given angle in degrees. """
rad = angle * math.pi / 180
cosa = math.cos(rad)
sina = math.sin(rad)
y = self.y * cosa - self.z * sina
z = self.y * sina + self.z * cosa
return Point3D(self.x, y, z)
def rotateY(self, angle):
""" Rotates the point around the Y axis by the given angle in degrees. """
rad = angle * math.pi / 180
cosa = math.cos(rad)
sina = math.sin(rad)
z = self.z * cosa - self.x * sina
x = self.z * sina + self.x * cosa
return Point3D(x, self.y, z)
def rotateZ(self, angle):
""" Rotates the point around the Z axis by the given angle in degrees. """
rad = angle * math.pi / 180
cosa = math.cos(rad)
sina = math.sin(rad)
x = self.x * cosa - self.y * sina
y = self.x * sina + self.y * cosa
return Point3D(x, y, self.z)
def project(self, win_width, win_height, fov, viewer_distance):
""" Transforms this 3D point to 2D using a perspective projection. """
factor = fov / (viewer_distance + self.z)
x = self.x * factor + win_width / 2
y = -self.y * factor + win_height / 2
return Point3D(x, y, 1)
class moc_orbit:
def __init__( self, line ):
''' a line from the SDSS MOC4 file. '''
''' assume that line is matched to astorb already '''
self._GM = 0.000295994511
### a* color
self._astar = float( line[29] )
### i-z color
self._iz = float( line[25] ) - float( line[27] )
self._RGB = get_color2(self._astar,self._iz)
### osculating elements
D2R = math.pi / 180.0
self._epoch = float( line[49] )
self._sma = float( line[50] )
self._ecc = float( line[51] )
self._inc = float( line[52] ) * D2R
self._node = float( line[53] ) * D2R
self._peri = float( line[54] ) * D2R
self._M = float( line[55] ) * D2R
self._tau = 2 * math.pi * math.sqrt( self._sma**3 / self._GM ) ### days!
### Absolute magnitude and phase-slope model
self._H = float( line[46] )
self._G = float( line[47] )
### rotation matrices - generate these beforehand, as they are static
self._P = self._sma * numpy.asarray( [ cos( self._peri ) * cos( self._node ) - sin( self._peri ) * cos( self._inc ) * sin( self._node ),
cos( self._peri ) * sin( self._node ) + sin( self._peri ) * cos( self._inc ) * cos( self._node ),
sin( self._peri ) * sin( self._inc ) ] )
self._Q = self._sma * sqrt( 1.0 - self._ecc**2 ) * numpy.asarray( [ -sin( self._peri ) * cos( self._node ) - cos( self._peri ) * cos( self._inc ) * sin( self._node ),
-sin( self._peri ) * sin( self._node ) + cos( self._peri ) * cos( self._inc ) * cos( self._node ),
sin( self._inc ) * cos( self._peri ) ] )
self._vkep = sqrt( self._GM / self._sma )
def pos( self, time_in, N=8 ):
''' General-purpose Keplerian -> Cartesian translator. '''
''' Array-ready, though does not do any idiot-proofing checks (yet). '''
''' Returns [ x, y, z ], [vx, vy, vz] '''
M = self._M + (time_in - self._epoch) * 2.0 * math.pi / self._tau
E = M + ( jv( 1, 1.0*self._ecc ) * sin( 1.0 * M ) * 2.0/float( 1.0 ) +
jv( 2, 2.0*self._ecc ) * sin( 2.0 * M ) * 2.0/float( 2.0 ) +
jv( 3, 3.0*self._ecc ) * sin( 3.0 * M ) * 2.0/float( 3.0 ) +
jv( 4, 4.0*self._ecc ) * sin( 4.0 * M ) * 2.0/float( 4.0 ) +
jv( 5, 5.0*self._ecc ) * sin( 5.0 * M ) * 2.0/float( 5.0 ) +
jv( 6, 6.0*self._ecc ) * sin( 6.0 * M ) * 2.0/float( 6.0 ) +
jv( 7, 7.0*self._ecc ) * sin( 7.0 * M ) * 2.0/float( 7.0 ) +
jv( 8, 8.0*self._ecc ) * sin( 8.0 * M ) * 2.0/float( 8.0 ) +
jv( 9, 9.0*self._ecc ) * sin( 9.0 * M ) * 2.0/float( 9.0 ) +
jv( 10, 10.0*self._ecc ) * sin( 10.0 * M ) * 2.0/float(10.0 ) )
### E is Eccentric Anomoly; we don't need True Anomoly for formalisms here.
rv = ( cos(E) - self._ecc ) * self._P + sin(E) * self._Q ### <-- Rotated [ x, y, z ]
return rv
def cameraspline( frame, breaktimes, breakvals ):
''' Smooth sinusoudal spline for camera position '''
if frame < min(breaktimes):
return breakvals[0]
if frame >= max(breaktimes):
return breakvals[-1]
i = 0
while breaktimes[i] <= frame:
i += 1
startval = breakvals[i-1]
endval = breakvals[i]
starttime = breaktimes[i-1]
endtime = breaktimes[i]
period = ( endtime - starttime )
amp = 0.5 * ( startval - endval )
func = amp * ( math.cos( math.pi * (frame - starttime)/period ) + 1.0 ) + endval
return func
def draw_ring( a ):
L = numpy.linspace(0,2.0 * math.pi, 1000 )
x,y = numpy.cos( L ) * a, numpy.sin( L ) * a
return x, y
def do_anim(core):
if not os.path.isdir('./MOC_MOVIE'):
print 'Setting up movie subdirectory ./MOC_MOVIE'
os.system('mkdir ./MOC_MOVIE')
### look for database version of ADR4 with orbit objects
database_exists = (os.path.isfile('ADR4.db.dat') or os.path.isfile('ADR4.db') or os.path.isfile('ADR4.db.db')) ### Crude handling of inconsistent behavior by 'shelve'
if not database_exists:
print 'reading data from ADR4.dat'
print 'Building database: WARNING - FILE PRODUCED WILL BE ROUGHLY 4.6 GB'
cont = raw_input('Continue? y/n: ').lower().strip()
if not cont[0] == 'y':
sys.exit(-1)
FILE = open('ADR4.dat', 'r')
orbs = []
already_match = set([]) ### <-- Hash table of objects that already exist
match_match = []
for LINE in FILE:
k = LINE.strip().split()
try:
if float( k[50] ) <= 0.0:
continue
s = '%s%s%s%s'%(k[50],k[51],k[52],k[53])
if s in already_match:
continue
else:
already_match.add(s)
if len(orbs)%10000 == 0:
print len(orbs), len(already_match)
this_orb = moc_orbit( k )
if this_orb._ecc > 0.8 or this_orb._sma > 7.0:
continue
orbs.append( this_orb )
except:
continue
FILE.close()
del already_match
print 'writing data to ADR4.db'
d = shelve.open('ADR4.db')
d['data'] = orbs
d.close()
else:
print 'reading data from ADR4.db'
d = shelve.open('ADR4.db')
orbs = d['data']
d.close()
print len(orbs), ' orbits read.'
### 16x9 figure, all black, no frames visible, set bbox=tight later to ensure crop
fig = pylab.figure(figsize=(16,9),frameon=False, facecolor='k', edgecolor='k')
ax = fig.add_axes([0,0,1,1], aspect='equal',axis_bgcolor='k', frameon=True)
### Initialize a few values
count = 0
scale0 = 10
angleX = 90.0 #90.0
fov = 5.0
N_cores = 8
if core != 0:
frames_for_this_core = numpy.arange(int(core),5000, N_cores)
else:
frames_for_this_core = numpy.arange(1,5000,1)
breaktimes_zoom = [ 0, 60*24, 100*24, 200 * 24 ]
breakvals_zoom = [ 0, 10.0, 3.0, 20.0 ]
breaktimes_angle = [ 0, 150 * 24 ]
breakvals_angle = [ 90.0, -180.0 ]
deltat_for_title = 7 * 24 ### < seven seconds of slop for title graphic
xEarth, yEarth = draw_ring( 1.0 )
xVenus, yVenus = draw_ring( 0.723 )
xMars, yMars = draw_ring( 1.523 )
xMerc, yMerc = draw_ring( 0.387 )
xJup, yJup = draw_ring( 5.204 )
planets = [ [xEarth, yEarth],
[xVenus, yVenus],
[xMars, yMars],
[xMerc, yMerc],
[xJup, yJup]]
for FRAME in range(1,4000 + deltat_for_title):
M = 51464.17418 + (FRAME-deltat_for_title) * 3.0 ### <- three-day timestep
angleX = cameraspline( FRAME-deltat_for_title, breaktimes_angle, breakvals_angle )
fov = cameraspline( FRAME-deltat_for_title, breaktimes_zoom, breakvals_zoom )
if not FRAME in frames_for_this_core or os.path.isfile('./MOC_MOVIE/tmp_%s.png'%(str(FRAME).rjust(5,'0')) ):
continue
x,y,s,c,zo=[],[],[],[],[]
s2, a2, rv = [],[],[]
time0 = time.time()
for orb in orbs:
### compute ecliptic cartesian coords
r = orb.pos( M )
### rotate for camera position
r0 = Point3D( r[0], r[1], r[2] )
rt = r0.rotateX(angleX)
### check to see if we should continue: is point in front of camera?
if rt.z > -fov:
### do perspective projection
p = rt.project(16.0, 9.0, 5.0, fov )
r2cam = ( rt.x**2 + rt.y**2 + (rt.z + fov)**2 )**0.5
rv.append( r2cam )
x.append( p.x )
y.append( p.y )
zo.append( -rt.z )
s.append( (2000.0/r2cam) * 10**( (5.0-orb._H) / 3.0 ) + 0.2 ) ### <- balance of rigorous point size and managing complexity.
c.append( orb._RGB )
ax.cla()
### draw 'rings' for four planets
for planet in planets:
xP,yP,zP = [],[],[]
for T in range(0, len(planet[0])):
r0 = Point3D( planet[0][T], planet[1][T], 0.0 )
rt = r0.rotateX(angleX)
if rt.z > -fov:
p = rt.project(16.0, 9.0, 5.0, fov )
xP.append( p.x )
yP.append( p.y )
zP.append( -rt.z )
ang_ratio = math.acos( abs( math.cos( angleX * math.pi / 180.0 ) ) ) * 180.0 / math.pi
ax.plot( xP, yP, 'w-', alpha = 0.5 * (1.0 - ang_ratio / 90.0)**0.5 , zorder=zP, lw=0.5 )
### compute 'bokeh' sizes
scale2cam = 4.0 + 4.0 / ( 1.0 + r2cam )
s2 = ( numpy.asarray( s )**0.5 * ( scale2cam ) )**2 + 1.0
time1 = time.time()
print 'Compute time: %.2f s'%( time1 - time0 )
### hard points
ax.scatter(x,y, s=s, alpha=1.0, edgecolor='none', c=c, zorder=zo)
### "bokeh" points
ax.scatter(x,y, s=s2, alpha=0.2, edgecolor='none', c=c, zorder=zo)
ax.set_xlim(0,16)
ax.set_ylim(0,9)
ax.set_xticks([])
ax.set_yticks([])
pylab.savefig('./MOC_MOVIE/tmp_%s.png'%(str(FRAME).rjust(5,'0')), bbox_inches='tight', pad_inches=0, dpi=120 )
time2 = time.time()
print 'Render time: %.2f s'%( time2 - time1 )
count += 1
if __name__ == "__main__":
try:
core = int( sys.argv[1] )
except:
print 'Error: expects core number (integer 1-8), or 0 to render all on single core.'
sys.exit(-1)
do_anim( core )