
David Ketcheson
Manuel Quezada de Luna
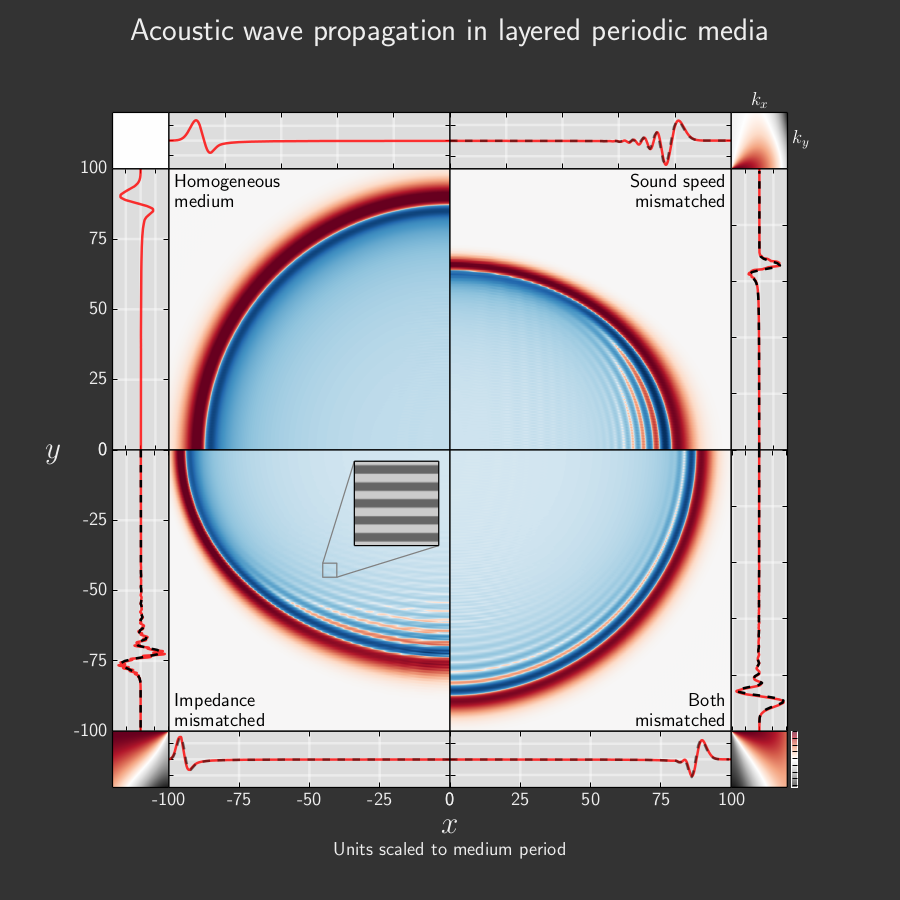
This figure presents results of simulations and analysis from the manuscript “Two- dimensional wave propagation in layered periodic media”, by Manuel Quezada de Luna and David I. Ketcheson (submitted; pre-print available). It shows how an initial Gaussian perturbation centered at the origin is propagated in a medium consisting of alternating horizontal layers of two different materials (the inset shows the structure of the medium). The four central plots show the two-dimensional wave behavior, while the adjacent line plots show traces of the solution along the lines \(x = 0\) and \(y = 0\). Each quadrant shows an experiment in a medium with different properties.
The top left plot shows the behavior in a homogeneous medium, consisting of an expanding wavefront with no dispersion. This is shown simply for reference.
In the bottom left plot, the layers have identical sound speeds but different impedances. Waves propagating in the vertical direction in this medium undergo repeated reflection and exhibit dispersion as a result. This is evident in the trace plot to the left, where the initial pulse has developed an oscillatory tail. This effect is fairly well understood.
The main subject of the manuscript is depicted in the top right plot, where the two layers have identical impedance, but different sound speeds. In this case there is no reflection, but waves traveling horizontally undergo diffraction. Remarkably, the large-scale effect of this diffraction is also to create an effective dispersion, as seen in the horizontal trace above the plot.
Finally, the bottom right plot involves a medium in which both the impedance and the sound speed vary. Effective dispersion is evident in both coordinate directions. The reflective dispersion happens to be more pronounced in this case, but in general either effect can be dominant, depending on the material properties.
The main plots and the red traces are the results of finite volume simulations of the variable-coefficient acoustic wave equation - with no dispersive terms. In the manuscript, a high order effective medium dispersive wave equation is derived by formal homogenization techniques. The black dotted lines are traces computed by solving these effective medium equations. Excellent agreement is observed in all cases.
Finally, the small plots in the corners show the effective dispersion relation for each medium, based on the effective medium equations. The effective sound speed is plotted as a function of the wavenumber components \(k_x, k_y\) . The axes of these plots are also oriented with the origin toward the center. As suggested by the central plots, it can be seen from the dispersion relations that low-frequency waves always travel fastest in the horizontal direction. But for high-frequency waves, propagation in the vertical can be faster if there is a large sound speed contrast and small impedance contrast.
Note that the straight horizontal lines that can be seen in some places are the effect of the medium structure, and have nothing to do with grid resolution, which is much too fine to be seen on the plot.